Outrageous Info About What Is 3 XOR 5

Unlocking the Secrets of 3 XOR 5

1. Understanding the Basics of XOR

Ever stumbled upon the term "XOR" and felt like you were deciphering an alien language? Don't worry, you're not alone! XOR, short for "exclusive or," is a logical operation that's actually quite simple once you get the hang of it. Think of it like this: it's a bit like a very picky bouncer at a club. Only one of two conditions can be true to get in, not both! It's all about finding the differences, not the similarities.

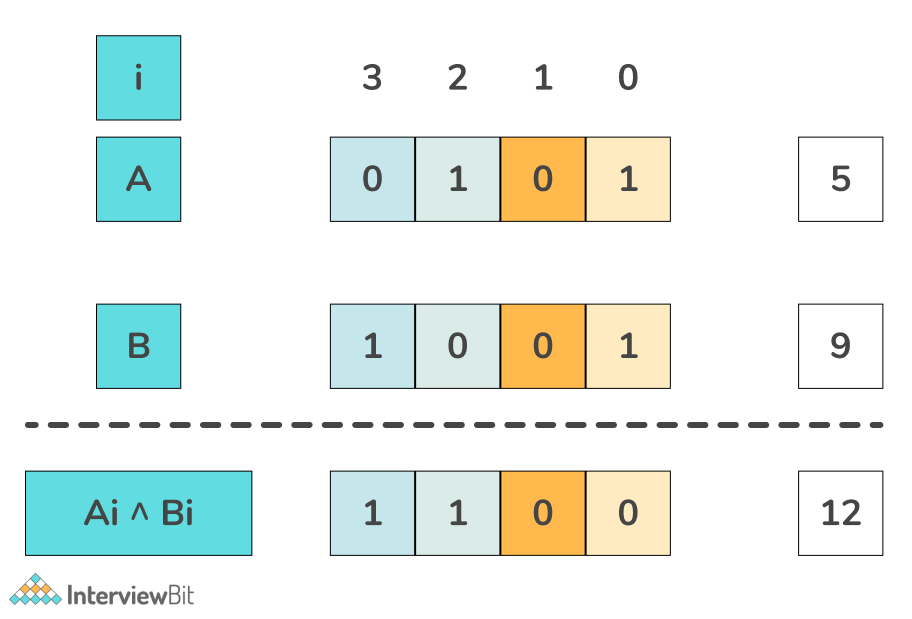
In the world of computers, XOR operates on binary numbers, which are just sequences of 0s and 1s. Each digit in a binary number is called a bit. So, 3 XOR 5 involves comparing the bits of the binary representations of 3 and 5.

Before we dive into the calculation, let's quickly recap how to convert decimal numbers (the numbers we use every day) to binary. The number 3 is 11 in binary (1 one and 1 two), and the number 5 is 101 in binary (1 one, 0 twos, and 1 four). Now, prepare for some bitwise action!

XOR is super helpful in cryptography, error detection, and even simple tasks like toggling switches. It's one of those fundamental concepts that pops up everywhere once you start looking. It's a core part of the toolbox of every computer scientist, so understanding it is like learning the secret handshake!

Diving Deep

2. The Bitwise Calculation Explained

Alright, let's break down 3 XOR 5 step by step. Remember, 3 is 11 in binary, and 5 is 101 in binary. Because the two numbers don't have same number of digits, we'll pad 3 (11) with a leading zero to become 011 to match the digit length of 5 (101). Now we can do the operation.

Here's the XOR truth table. 0 XOR 0 = 0, 0 XOR 1 = 1, 1 XOR 0 = 1, and 1 XOR 1 = 0. Armed with this knowledge, we can compare the bits of 011 and 101:

• First bit: 0 XOR 1 = 1
• Second bit: 1 XOR 0 = 1
• Third bit: 1 XOR 1 = 0

Putting these results together, we get 110 in binary. Convert this back to decimal, and what do we have? 6! So, 3 XOR 5 = 6. Mystery solved! You've officially conquered your first XOR operation. Celebrate with a digital high-five!

It's essential to remember that XOR looks for the differences, not the similarities. If the bits are the same (both 0 or both 1), the result is 0. If they're different, the result is 1. This simple rule is the key to understanding XOR's power.

Why is XOR Important Anyway?

3. Real-World Applications of XOR

You might be thinking, "Okay, I can calculate 3 XOR 5, but why should I care?" Well, XOR has some seriously cool applications. One of the most common is in cryptography. XOR can be used to encrypt data by combining it with a key. The encrypted data can then be decrypted by XORing it with the same key again. It's a simple but effective way to protect sensitive information.

Another application is in error detection. XOR can be used to calculate parity bits, which are extra bits added to a data stream to detect errors. If an error occurs during transmission, the parity bit will be incorrect, and the error can be detected.

XOR also shows up in image manipulation. For example, you can use XOR to create interesting visual effects by combining two images. Or, you can use it to perform simple tasks like toggling the color of pixels.

Beyond these specific examples, XOR is a fundamental building block in computer science. It's used in countless algorithms and data structures. Understanding XOR is like learning a fundamental law of nature in the digital world. It opens up a whole new way of thinking about and manipulating data.

XOR in Programming Languages

4. How to Use XOR in Code

Most programming languages have a built-in XOR operator. In many languages, like C++, Java, and Python, the XOR operator is represented by the caret symbol (^). So, to calculate 3 XOR 5 in Python, you would simply write `3 ^ 5`.

Here's a little code snippet to illustrate:

# Python code to calculate 3 XOR 5a = 3b = 5result = a ^ bprint(result) # Output: 6

It's that easy! You can use XOR in your own programs to perform all sorts of interesting operations. Experiment with different values and see what happens. Once you understand the basics, you can start to explore more advanced uses of XOR.

Different languages might have slightly different ways of handling XOR, especially when dealing with different data types. But the underlying principle remains the same: it's all about bitwise comparison and finding the differences.

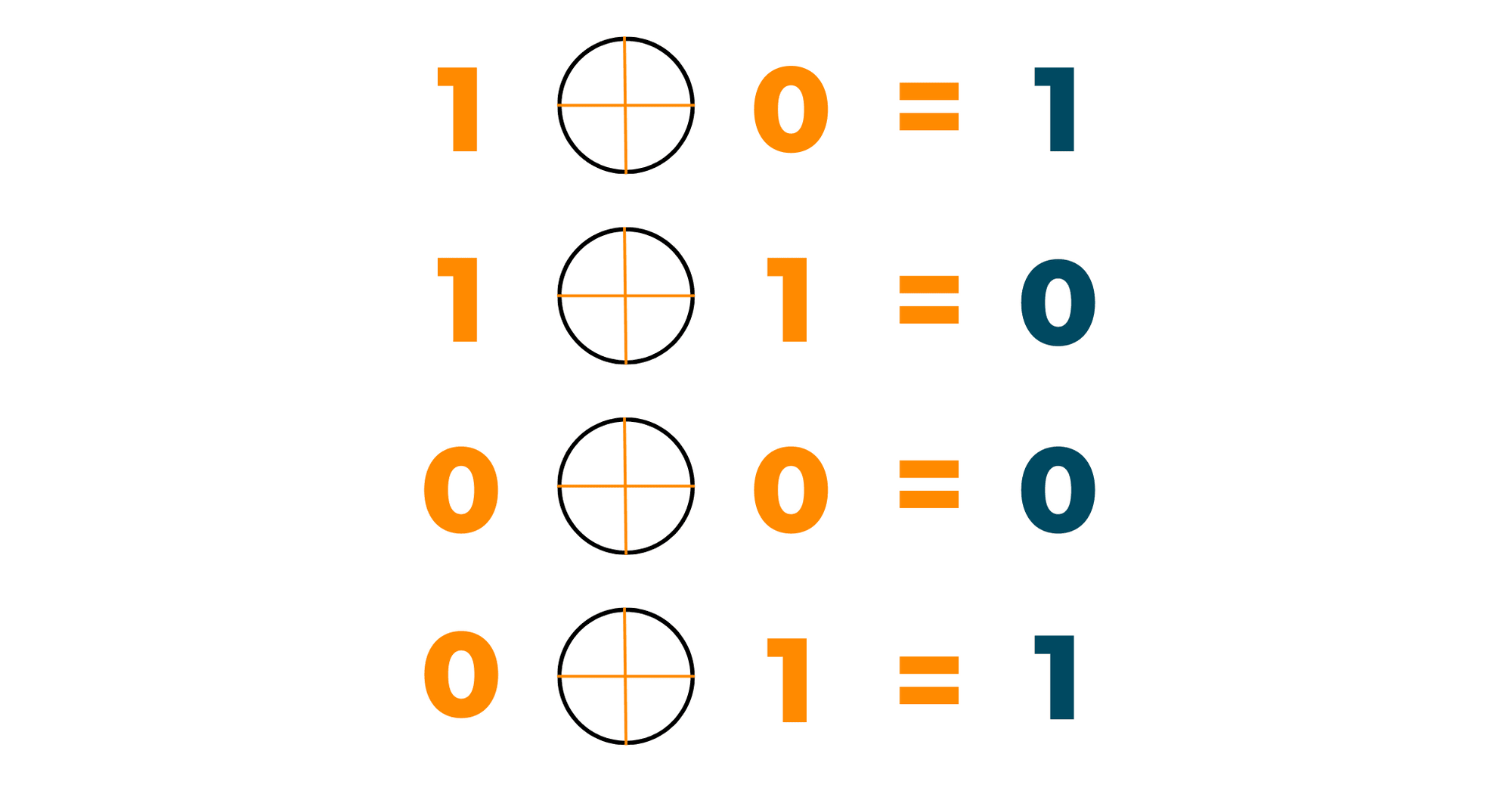
Beyond the Basics

5. Delving Deeper into XOR's Capabilities

Once you've mastered the basics of XOR, you can start exploring more advanced topics. For example, you can learn about XOR linked lists, which are a memory-efficient way to implement linked lists. Or, you can investigate XOR ciphers, which are a type of encryption algorithm based on XOR.

The possibilities are endless. XOR is a powerful tool that can be used in a wide variety of applications. As you continue your journey in computer science, you'll undoubtedly encounter XOR again and again. So, take the time to understand it well. It's an investment that will pay off in the long run.

So, there you have it — the lowdown on 3 XOR 5! Hopefully, this article has demystified XOR and shown you how useful it can be. Keep exploring, keep experimenting, and keep learning. The world of computer science is full of fascinating concepts just waiting to be discovered.

And remember, even the most complex concepts can be broken down into simple, understandable steps. Just take it one bit at a time!

Frequently Asked Questions (FAQs) About XOR

6. Your Burning Questions Answered

Still have some questions about XOR? No problem! Here are a few frequently asked questions to help clear things up:

Q: What happens if I XOR a number with itself?

A: If you XOR a number with itself, the result will always be 0. This is because every bit will be the same, and XOR only returns 1 if the bits are different.

Q: Is XOR commutative?

A: Yes, XOR is commutative. This means that the order of the operands doesn't matter. So, `a XOR b` is the same as `b XOR a`.

Q: Can XOR be used with numbers other than integers?

A: XOR is typically used with integers because it operates on the individual bits of the numbers. However, in some contexts, it can be extended to other data types by treating them as sequences of bits.

Q: What does "bitwise" mean?

A: "Bitwise" means that an operation is performed on each individual bit of a number. So, a bitwise XOR operation compares the corresponding bits of two numbers and produces a new number where each bit is the result of the XOR operation on the corresponding bits of the original numbers.